Sliding ladder
1 Introduction
This a problem I recently discovered on StackOverflow. Here is a typical question related to this subject: “A \(L\) meters ladder is resting on a wall, so that the top of the ladder is \(y_0\) meters above the ground and the bottom of the ladder is \(x_0\) meters from the wall. At some time, the ladder is slipping so that the top of the ladder falls at a constant rate of \(v_y~m.min^{-1}\). How fast is the bottom of the ladder slipping away from the wall?”
Surprisingly, this problem can be solved without invoking kinetic or potential energy as the ladder fall rate is given. Therefore it is only mathematics but this remains interesting to me and possibly to other people that are not accustomed to ladders.
2 Model
The ladder-situation is represented below:
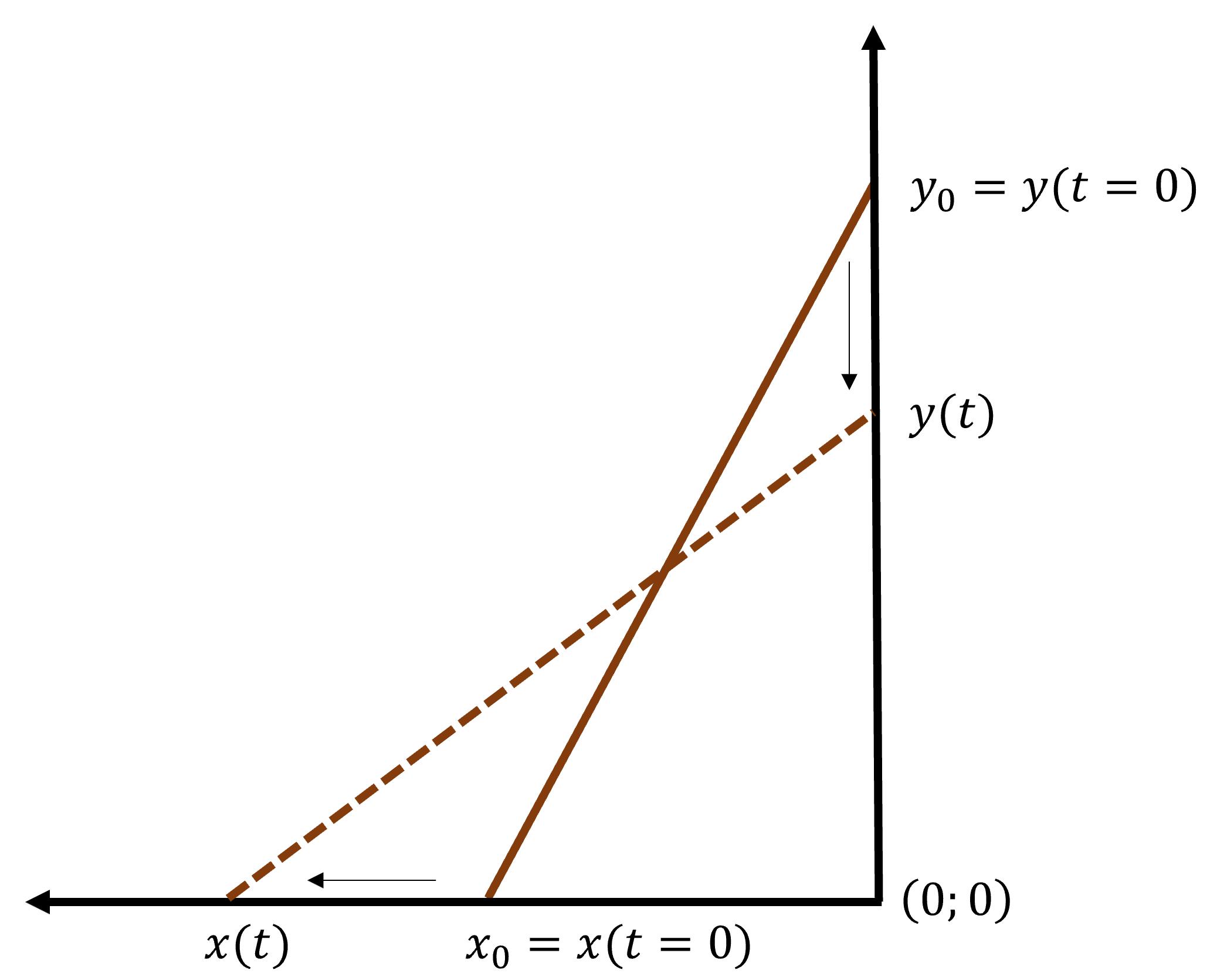
Figure 2.1: Ladders’s position evolution among time.
The brown line is the ladder at its initial state while the dashed line represent the ladder position at an arbitrary time \(t\).
At any time the ladder position must respect the following constraint:
\[\begin{equation} x\left(t\right)^2 + y\left(t\right)^2 = L^2 \tag{2.1} \end{equation}\]
The indication that the ladder falls at a constant speed allows us to write:
\[\begin{equation} y\left(t\right) = y_0 - t \times v_y \tag{2.2} \end{equation}\]
Therefore, \(x\) variation with respect to time is:
\[\begin{equation} \begin{aligned} x\left(t\right) &= \sqrt{L^2 - y\left(t\right)^2}\\ &= \sqrt{L^2 - \left(y_0 - t \times v_y\right)^2}\\ &= \sqrt{L^2 - y_0^2 + 2y_0v_yt - t^2 v_y^2} \end{aligned} \tag{2.3} \end{equation}\]
From this expression one can immediately derive the slipping speed of the ladder \(v_x\):
\[\begin{equation} v_x\left(t\right) = \frac{dx}{dt} = \frac{tv_y^2 - y_0 v_y}{\sqrt{L^2 - y_0^2 + 2y_0v_yt - t^2 v_y^2}} \tag{2.4} \end{equation}\]
Another way to obtain this expression is to derive Equation (2.1) with respect to time:
\[\begin{equation} 2x \times \frac{dx}{dt} + 2y \times \frac{dy}{dt} = 0 \tag{2.5} \end{equation}\]
This equation can be simplified:
\[\begin{equation} x\left(t\right) v_x\left(t\right) + y\left(t\right) v_y = 0 \tag{2.6} \end{equation}\]
Therefore:
\[\begin{equation} v_x\left(t\right) = -\frac{y\left(t\right)v_y}{x\left(t\right)} = \frac{tv_y^2 - y_0 v_y}{\sqrt{L^2 - y_0^2 + 2y_0v_yt - t^2 v_y^2}} \tag{2.7} \end{equation}\]