3.1 Derivation of \(OC\) expression

One can see in triangle \(OCE\) that:

\[\begin{equation} \sin{\left(\alpha+\theta\right)} = \frac{OC}{OE} \Leftrightarrow OC = OE \times \sin{\left(\alpha+\theta\right)} \tag{3.2} \end{equation}\]

Moreover, in triangle \(OBE\):

\[\begin{equation} \cos{\alpha} = \frac{b}{OE} \Leftrightarrow OE = \frac{b}{\cos{\alpha}} \tag{3.3} \end{equation}\]

Combining (3.2) and (3.3), one finds:

\[\begin{equation} OC = b\times \frac{\sin{\left(\alpha+\theta\right)}}{\cos{\alpha}} \tag{3.4} \end{equation}\]

We want to get ride of the \(\alpha\) terms to only have an expression using \(\theta\) (otherwise we will have too many unknowns for the set of equations derived from Newton’s second law). One can remember that \(\sin{\left(\alpha+\theta\right)} = sin{\alpha} \cos{\theta} + sin{\theta} \cos{\alpha}\). Therefore, (3.4) becomes:

\[\begin{equation} OC = b\times \frac{sin{\alpha} \cos{\theta} + sin{\theta} \cos{\alpha}}{\cos{\alpha}} = b\times \left(tan{\alpha} \cos{\theta} + sin{\theta}\right) \tag{3.5} \end{equation}\]

Now only \(\tan{\alpha}\) remains to be removed. By looking at triangle \(OBE\), one sees that:

\[\begin{equation} \tan{\alpha} = \frac{BE}{b} \tag{3.6} \end{equation}\]

And by looking at triangle \(BEP\), one finds that:

\[\begin{equation} cos{\theta} = \frac{l}{BE} \tag{3.7} \end{equation}\]

Therefore, combining equations (3.6) and (3.7), one finds that:

\[\begin{equation} \tan{\alpha} = \frac{l}{b \cos{\theta}} \tag{3.8} \end{equation}\]

Finally, the \(OC\) expression from (3.5) becomes:

\[\begin{equation} OC = b \times \left(\frac{l}{b\cos{\theta}} \times \cos{\theta}+ \sin{\theta}\right) = l+b \sin{\theta} \tag{3.9} \end{equation}\]

3.2 Derivation of \(CP\) expression

In triangle \(OCE\), one can derive:

\[\begin{equation} \cos{\alpha+\theta} = \frac{CE}{OE} = \frac{CE \cos{\alpha}}{b} \Leftrightarrow CE = b \times \frac{\cos{\alpha+\theta}}{\cos{\alpha}} \tag{3.10} \end{equation}\]

One can remember that \(\cos{\left(\alpha+\theta\right)} = cos{\alpha} \cos{\theta} - sin{\theta} \sin{\alpha}\). Therefore:

\[\begin{equation} CE = b \times \frac{cos{\alpha} \cos{\theta} - sin{\theta} \sin{\alpha}}{\cos{\alpha}} = b \times \left(\cos{\theta} - \sin{\theta} \tan{\alpha}\right) \tag{3.11} \end{equation}\]

Injecting equation (3.8) in (3.11):

\[\begin{equation} CE = b \times \left(\cos{\theta} - \sin{\theta} \frac{l}{b \cos{\theta}}\right) = b \cos{\theta} - l \tan{\theta} \tag{3.12} \end{equation}\]

Because \(CP = CE + EP\) and that in triangle \(BEP\) one sees that \(\tan{\theta} = EP/l\) one finally finds:

\[\begin{equation} CP = b \cos{\theta} - l \tan{\theta} + l \tan{\theta} = b \cos{\theta} \tag{3.13} \end{equation}\]

From equations (3.9) and (3.13), one has:

\[\begin{equation} \overrightarrow{OP} = \left(l+b \sin{\theta}\right) \times \left(-\overrightarrow{e}_{\theta}\right) + b \cos{\theta} \times \left(-\overrightarrow{e}_{r}\right) \tag{3.14} \end{equation}\]

3.3 Expression of \(\overrightarrow{OP}\) derivatives with respect to time

The unit vectors \(\overrightarrow{e}_{r}\) and \(\overrightarrow{e}_{\theta}\) will move with time. Indeed, the direction of these vectors is directly related to the value of \(\theta\) which varies with time. Therefore, these vectors must be derived when the derivatives of \(\overrightarrow{OP}\) will be calculated. To find these derivatives, the simplest is to express \(\overrightarrow{e}_{r}\) and \(\overrightarrow{e}_{\theta}\) in the other referential defined by vectors \(\overrightarrow{e}_{x}\) and \(\overrightarrow{e}_{y}\) which do not move with time. From figure 3.1, one can see that:

\[\begin{equation} \overrightarrow{e}_{\theta} = -\sin{\theta} \times \overrightarrow{e}_{x} - \cos{\theta} \times \overrightarrow{e}_{y} \tag{3.15} \end{equation}\]

and

\[\begin{equation} \overrightarrow{e}_{r} = -\cos{\theta} \times \overrightarrow{e}_{x} + \sin{\theta} \times \overrightarrow{e}_{y} \tag{3.16} \end{equation}\]

Therefore, \(d\overrightarrow{e}_{\theta}/dt\) and \(d\overrightarrow{e}_{r}/dt\) can be calculated:

\[\begin{equation} \frac{d\overrightarrow{e}_{\theta}}{dt} = -\dot{\theta}\cos{\theta} \times \overrightarrow{e}_{x} + \dot{\theta}\sin{\theta} \times \overrightarrow{e}_{y} = \dot{\theta} \times \overrightarrow{e}_{r} \tag{3.17} \end{equation}\]

and

\[\begin{equation} \frac{d\overrightarrow{e}_{r}}{dt} = \dot{\theta}\sin{\theta} \times \overrightarrow{e}_{x} + \dot{\theta}\cos{\theta} \times \overrightarrow{e}_{y} = - \dot{\theta} \times \overrightarrow{e}_{\theta} \tag{3.18} \end{equation}\]

Now, one can calculate the first derivative of \(\overrightarrow{OP}\) derivatives with respect to time:

\[\begin{equation} \frac{d\overrightarrow{OP}}{dt} = \left(\dot{b} \sin{\theta} + b\dot{\theta}\cos{\theta}\right) \times \left(-\overrightarrow{e}_{\theta}\right) + \left(l+b\sin{\theta}\right)\times\left(-\dot{\theta} \times \overrightarrow{e}_{r}\right) + \left(\dot{b}\cos{\theta} - b\dot{\theta}\sin{\theta}\right) \times \left(-\overrightarrow{e}_{r}\right) + b \cos{\theta} \times \dot{\theta} \times \overrightarrow{e}_{\theta} \tag{3.19} \end{equation}\]

Some terms cancel. Once the simplifications are done, one obtains:

\[\begin{equation} \frac{d\overrightarrow{OP}}{dt} = -\dot{b} \sin{\theta} \times \overrightarrow{e}_{\theta}+ \left(-l\dot{\theta} - \dot{b}\cos{\theta}\right) \times \overrightarrow{e}_{r} \tag{3.20} \end{equation}\]

The second derivative of \(\overrightarrow{OP}\) can be calculated:

\[\begin{equation} \frac{d^2\overrightarrow{OP}}{dt^2} = \left(-\ddot{b}\sin{\theta}-\dot{b}\dot{\theta}\cos{\theta}\right) \times \overrightarrow{e}_{\theta} - \dot{b} \dot{\theta} \sin{\theta} \times\overrightarrow{e}_{r} + \left(-l\ddot{\theta} - \ddot{b}\cos{\theta} + \dot{b}\dot{\theta} \sin{\theta}\right) \times\overrightarrow{e}_{r} - \left(-l\dot{\theta} - \dot{b}\cos{\theta}\right) \dot{\theta} \times \overrightarrow{e}_{\theta} \tag{3.21} \end{equation}\]

Once the simplifications are done, one obtains:

\[\begin{equation} \frac{d^2\overrightarrow{OP}}{dt^2} = \left(-\ddot{b}\sin{\theta} + l \dot{\theta}^2\right) \times \overrightarrow{e}_{\theta} + \left(-l\ddot{\theta} - \ddot{b}\cos{\theta}\right) \times\overrightarrow{e}_{r} \tag{3.22} \end{equation}\]

6.1 Small oscillations

In the case of small oscillations, \(\theta\) will remain close to zero and under this assumption, \(\sin{\theta} \approx \theta\) and \(\cos{\theta} \approx 1\). Therefore, equation (5.6) becomes:

\[\begin{equation} \ddot{\theta} + \frac{g}{l} \theta + \frac{\ddot{b}}{l} = 0 \tag{6.1} \end{equation}\]

According to Wolfram Alpha, the solution of this differential equation is:

\[\begin{equation} \theta\left(t\right) = \underbrace{C_1 \sin{\left(\sqrt{\frac{g}{l}}t\right)} + C_2 \cos{\left(\sqrt{\frac{g}{l}}t\right)}}_{\text{static pendulum classical solution}} + \sin{\left(\sqrt{\frac{g}{l}}t\right)} \int_1^t{-\frac{\ddot{b}\left(\xi\right) \cos{\left(\frac{g}{l}\xi\right)}}{\sqrt{gl}} d\xi} + \cos{\left(\sqrt{\frac{g}{l}}t\right)} \int_1^t{\frac{\ddot{b}\left(\xi\right) \sin{\left(\frac{g}{l}\xi\right)}}{\sqrt{gl}} d\xi} \tag{6.2} \end{equation}\]

It is likely that the integrals might not have an analytical solution depending on the \(\ddot{b}\) expression used. Therefore, numerical resolution will have to be performed, even for the small oscillations problem.

6.2 Constant angle

If one wants to know what the \(\ddot{b}\) expression must be so that the pendulum angle does not move, one can solve equation (5.6) with \(\theta=\theta_0\) with \(\theta_0\) the pendulum angle at the initial time. Therefore:

\[\begin{equation} \frac{g}{l} \sin{\theta_0} + \frac{\ddot{b}}{l}\cos{\theta_0} = 0 \tag{6.3} \end{equation}\]

Therefore, \(\ddot{b}\) is:

\[\begin{equation} \ddot{b} = -g\tan{\theta_0} \tag{6.4} \end{equation}\]

The solution to this differential equation, assuming an initially still board and centered in \(x=0\) is:

\[\begin{equation} b\left(t\right) = -\frac{1}{2}gt^2\tan{\theta_0} \tag{6.4} \end{equation}\]

It is interesting to notice that this equation diverges when \(\theta_0=\pi/2\) (i.e., it is not possible to maintain a constant angle of 90° for the pendulum).

7.1 Python code

Only few parameters should be changed for your personal use:

• HISTORY_LEN to adjust simulation time
• board_function(t) to define your own board movement equation
• LENGTH for the rope length

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from collections import deque

# Constants
HISTORY_LEN = 500  # Number of trajectory points to display
TEND = 20  # Simulation time in s
DT = 0.02  # Calculation interval in s
NSTEP = int(TEND / DT)


def board_function(t):
    return np.sin(t)


def second_derivative_board_function(t):
    eps = DT / 100
    return (board_function(t + eps) - 2 * board_function(t) + board_function(t - eps)) / eps ** 2


def pendulum_ode(y, t, gravity, length):
    theta, theta_dot = y
    dydt = [theta_dot, -gravity / length * np.sin(theta) - second_derivative_board_function(t) / length * np.cos(theta)]
    return dydt


def animate(time_step):
    thisx = [xb[time_step], xp[time_step]]
    thisy = [yb[time_step], yp[time_step]]

    if time_step == 0:
        history_x.clear()
        history_y.clear()

    history_x.appendleft(thisx[1])
    history_y.appendleft(thisy[1])

    line.set_data(thisx, thisy)
    trace.set_data(history_x, history_y)
    time_text.set_text(time_template % (time_step * DT))
    return line, trace, time_text


if __name__ == '__main__':
    t = np.linspace(0, TEND, NSTEP)
    y0 = [np.pi/4, 0]
    GRAVITY = 9.81  # m.s-2
    LENGTH = 1  # m

    sol = odeint(pendulum_ode, y0, t, args=(GRAVITY, LENGTH))

    # Calculate coordinates
    xb = [board_function(ti) for ti in t]
    yb = [0] * len(t)
    xp = [board_function(ti) + LENGTH * np.sin(sol[i, 0]) for i, ti in enumerate(t)]
    yp = [-LENGTH * np.cos(sol[i, 0]) for i in range(len(sol[:, 0]))]

    # xp = xp / np.max(np.abs(xb))
    # xb = xb / np.max(np.abs(xb))

    fig = plt.figure(figsize=(10, 10))

    # Calculate bmin and bmax
    bmin = min(xb)
    bmax = max(xb)

    ax = fig.add_subplot(autoscale_on=False, xlim=(bmin-LENGTH, bmax+LENGTH), ylim=(-LENGTH, LENGTH))
    ax.set_aspect('equal')
    ax.grid()

    line, = ax.plot([], [], 'o-', lw=2)
    trace, = ax.plot([], [], '.-', lw=1, ms=2)
    time_template = 'time = %.1fs'
    time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
    history_x, history_y = deque(maxlen=HISTORY_LEN), deque(maxlen=HISTORY_LEN)

    ani = animation.FuncAnimation(fig, animate, len(sol[:, 0]), interval=DT * 500, blit=True)
    plt.show()

7.2 Results

The pendulum length was assumed to be 1 meter for all simulations but the last one. Indeed, in order to have a plot of acceptable size, I needed to assume a pendulum of 1 km. However, the result should not be impacted by this change.

7.2.1 Still board

• Initial pendulum angle is 45° (cf. figure 7.1): an oscillation of the pendulum is obtained. So far, no surprise, it was just to check that the calculation was consistent for this simple case.

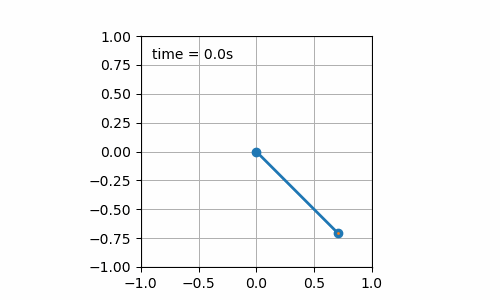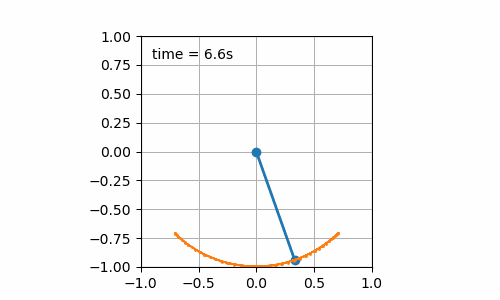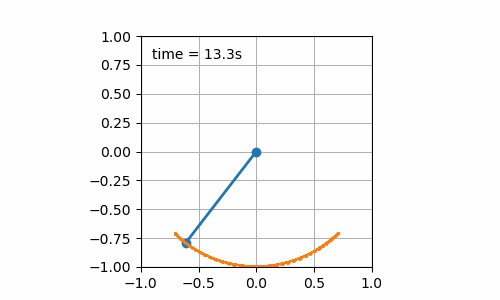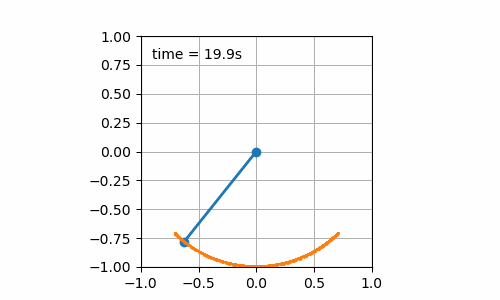
Figure 7.1: Still board with initial pendulum angle of 45°

• Initial pendulum angle is 180° (cf. figure 7.2). The pendulum is stable for the 20 seconds of simulation. I was not sure that it would be the case as numerical errors do exist and could have increased leading to reaching a value of the pendulum angle slightly different from 180°, yet sufficient, to initiate a swing. This setup is known as the inverse pendulum.

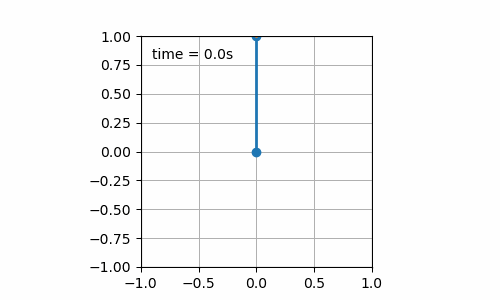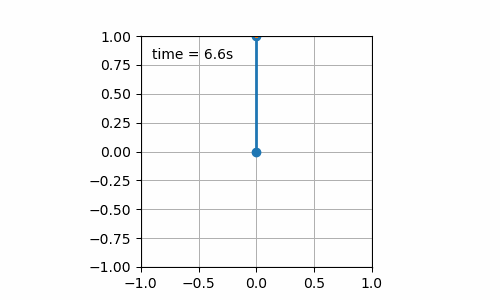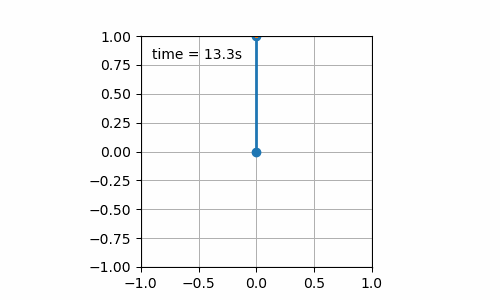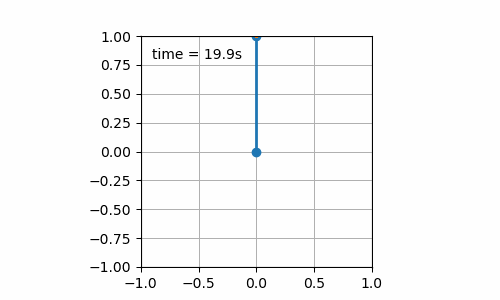
Figure 7.2: Still board with initial pendulum angle of 180°

7.2.2 Moving board

• Sinusoidal displacement of the board (\(b\left(t\right) = \sin\left(t\right)\)) with initial pendulum angle of 45° (cf. figure 7.3). Here starts the fun. It seems that for this condition, the pendulum describes a “bretzel” shape. Not enough to win a Nobel prize, yet fun to see 😁.

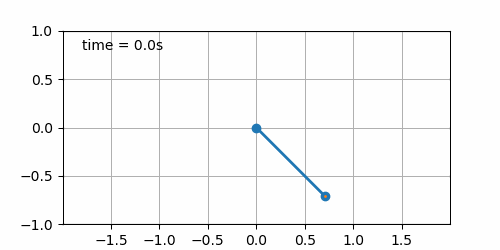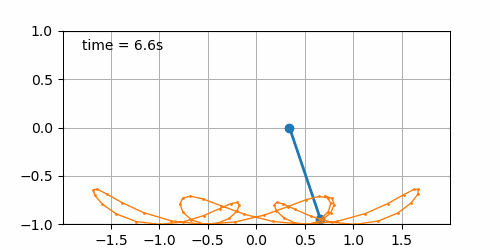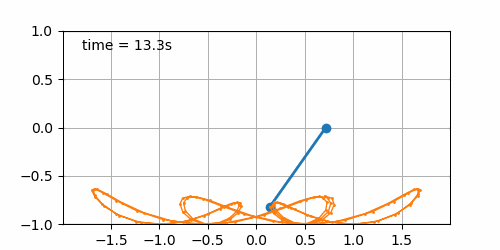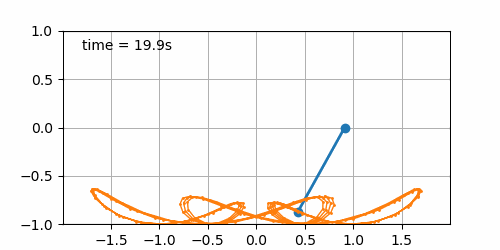
Figure 7.3: Sinusoidal board movement with initial pendulum angle of 45°

• Sinusoidal displacement of the board (\(b\left(t\right) = \sin\left(t\right)\)) with initial pendulum angle of 90° (cf. figure 7.4). It is interesting to observe that the pattern drawn by the pendulum is different when changing its initial angle. Again, nothing amazing but I have the intuition that it should be possible to draw some nice pictures with a nice set of conditions (initial pendulum angle, board displacement over time).

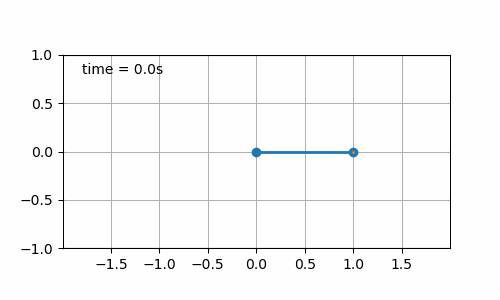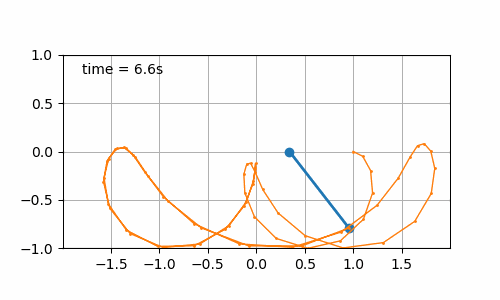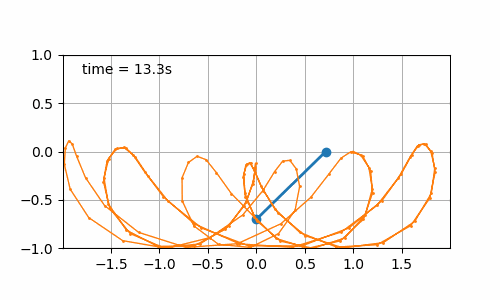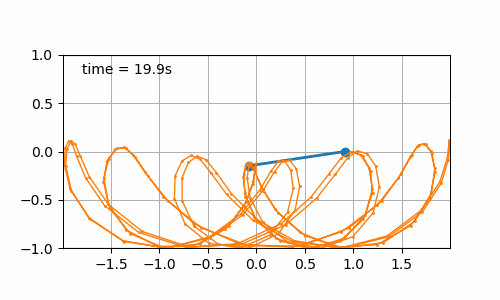
Figure 7.4: Sinusoidal board movement with initial pendulum angle of 90°

• Sinusoidal displacement of the board (\(b\left(t\right) = \sin\left(t\right) + \sin\left(t/3\right)\)) with initial pendulum angle of 45° (cf. figure 7.5). With this one it is interesting to see that the combination of two sinus curves to express the board displacement can already lead to complex patters for the pendulum movement. I believe that the coefficients of the sinus terms from the board displacement equation can be estimated performing the harmonic analysis of the pendulum position over time. Maybe for a next time.

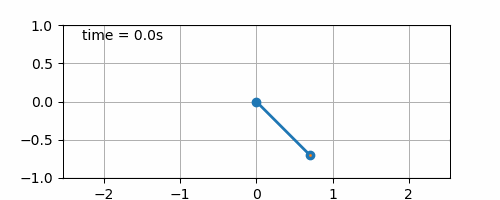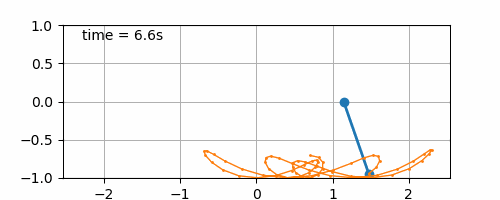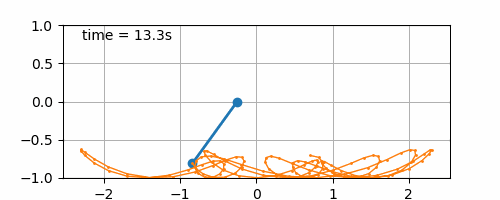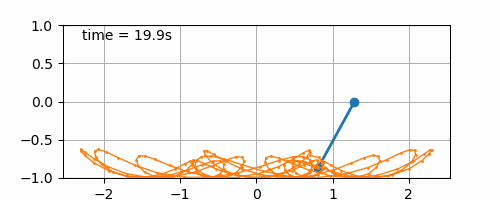
Figure 7.5: Double sinusoidal board movement

• Constant angle solution (cf. figure 7.6). The initial pendulum angle is set to 45°. This one was just to check that equation (6.4) was correct. And yes it is 😎.

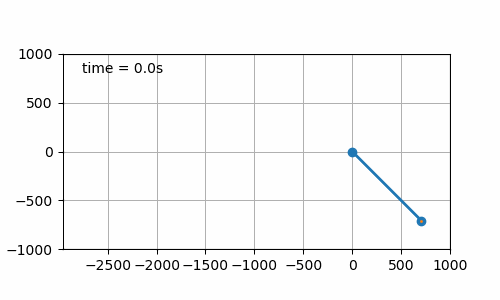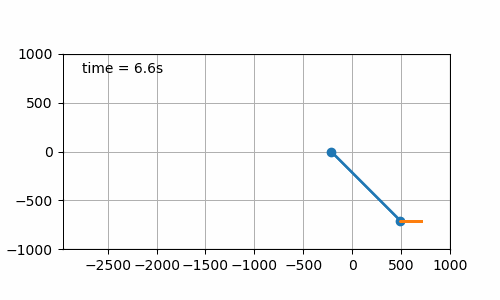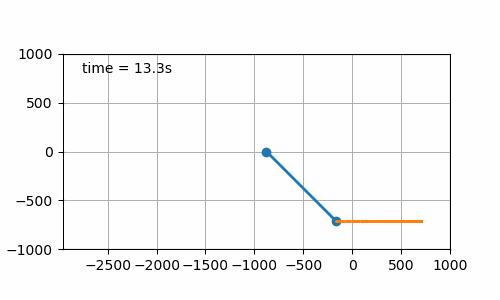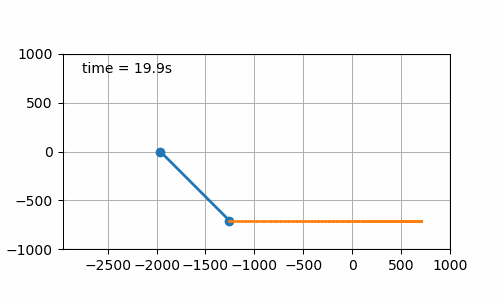
Figure 7.6: Board displacement to maintain pendulum angle